引言
射频频率稳定度是衡量振荡器在复杂电磁环境中维持输出频率恒定能力的核心指标,直接影响通信系统信号传输质量、雷达测速精度及卫星导航定位准确性。传统频率稳定度评估依赖频域相位噪声分析,但面对现代电子系统对短期稳定度的严苛要求,时域分析方法逐渐成为研究热点。阿伦方差作为时域稳定性评估工具,通过量化频率数据的随机波动特性,为射频器件性能优化提供了关键理论支撑。本文将从理论、计算方法及应用三个维度,系统对比阿伦方差与传统标准方差的差异,并深入探讨阿伦方差在射频频率稳定度评估中的技术优势。
一、射频频率稳定度的物理内涵与技术挑战
1.1 频率稳定度的双维度表征
频率稳定度分为长期稳定度与短期稳定度。长期稳定度由元件老化(如晶体谐振器年老化率达±1 ppb)和环境温漂主导,需通过恒温晶振(OCXO)或温度补偿技术抑制;短期稳定度则反映毫秒至秒级频率起伏,主要受电路噪声(热噪声、闪烁噪声)和电源波动影响。在5G基站中,频率稳定度需优于0.1 ppm以保障低误码率传输。
1.2 相位噪声与频率稳定度的关联
频域表征采用单边带相位噪声(SSB),定义为偏离载频Δf处单位带宽噪声功率与载波功率比值。例如,某1 GHz振荡器在偏离载频1 kHz处相位噪声为-95 dBc/Hz,对应短期频率稳定度。时域与频域表征互补:频域分析适用于高频噪声,时域阿伦方差更擅长捕捉低频噪声特性。
二、阿伦方差与标准方差的理论对比
2.1 核心目标差异
标准方差通过计算数据与均值的偏离程度,反映整体离散性,其公式为: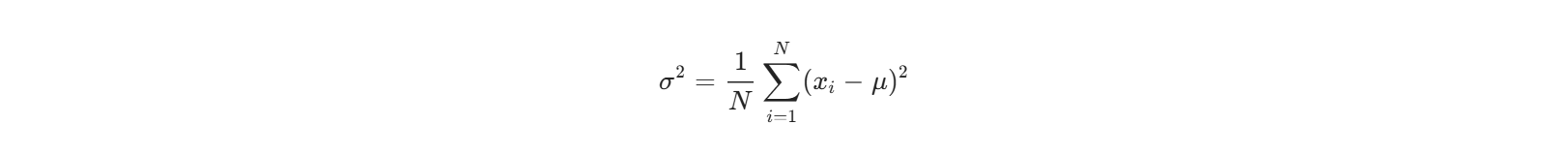
而阿伦方差通过分块平均和差分运算,聚焦于特定时间尺度的稳定性,其公式为: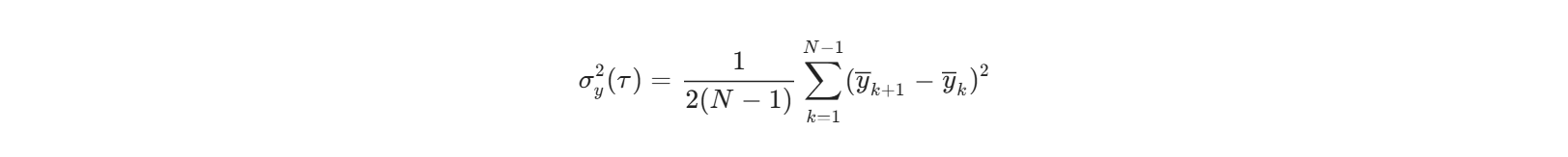
标准方差将所有时间尺度的波动混合计算,而阿伦方差通过调整块长度τ,可分离不同时间尺度的噪声成分。
2.2 噪声类型辨识能力
标准方差无法区分噪声类型,而阿伦方差曲线斜率与噪声类型存在对应关系:
斜率-1:白相位噪声(受热噪声主导)
斜率0:闪烁相位噪声(1/f噪声)
斜率+1:白频率噪声(随机游走)
例如,某铷原子钟的阿伦方差曲线显示,在τ=1 s时斜率为-1,表明短期稳定度受热噪声限制;在τ=100 s时斜率为0,表明中长期漂移由1/f噪声主导。
2.3 收敛性对比
标准方差对时变噪声(如1/f噪声)可能不收敛,而阿伦方差对各类噪声的幂律谱项均收敛,适合分析非平稳信号。这一特性使其在时频计量领域(如原子钟、晶振)具有不可替代的优势。
三、阿伦方差与标准方差的计算方法对比
3.1 数据处理流程
标准方差直接计算数据与均值的差的平方和,而阿伦方差通过以下步骤实现:
分段平均:将数据划分为N个区间,计算每个区间均值:
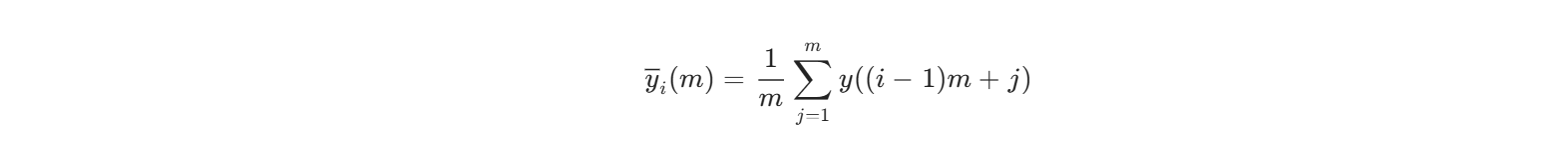
差分运算:计算相邻区间均值差:
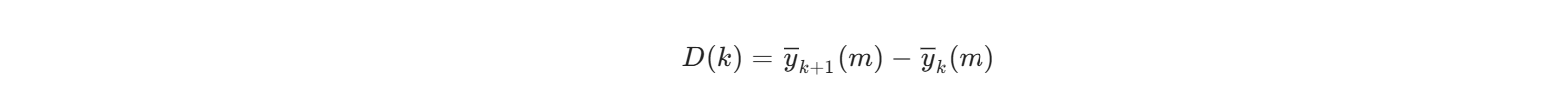
方差统计:
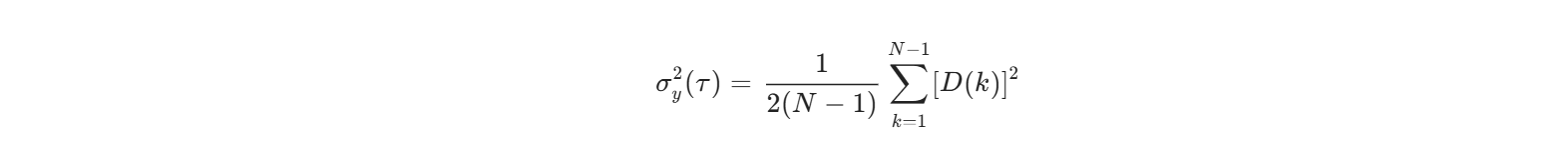
3.2 时间尺度敏感性
标准方差为单一值,不区分时间尺度;阿伦方差通过改变块长度τ,可分析不同时间尺度的稳定性。例如,在射频器件测试中,τ=1 s反映短期抖动,τ=1000 s反映长期漂移。
3.3 计算复杂度
标准方差计算复杂度为O(N),而阿伦方差因需分段和差分运算,复杂度为O(N log N)。但随着计算资源提升,这一差异在工程实践中已可忽略。
四、阿伦方差与标准方差的应用对比
4.1 适用场景
标准方差:通用数据分析,如质量控制、金融风险评估。例如,在生产线上,通过计算产品尺寸的标准方差,可监控生产过程的稳定性。
阿伦方差:时频计量(如原子钟、晶振)、惯性导航(如陀螺仪、加速度计)的稳定性评估。例如,在卫星导航系统中,阿伦方差用于预测惯性器件的累积误差,推算系统定位精度上限。
4.2 工程实践案例
标准方差应用:在射频功率放大器测试中,通过计算输出功率的标准方差,可评估其线性度。某型GaN功率放大器的输出功率标准方差为0.5 dB,表明其功率稳定性良好。
阿伦方差应用:在某型铷原子钟测试中,阿伦方差曲线显示,在τ=1 s时σ_y(τ)=2.1×10⁻⁹,表明其短期稳定度优异;在τ=1000 s时σ_y(τ)=1.8×10⁻⁸,表明需通过温控技术抑制长期漂移。
4.3 优势总结
标准方差:计算简单,直观反映数据分散程度,适用于通用数据分析。
阿伦方差:提供时间尺度相关的稳定性信息,指导器件选型与系统设计,尤其在射频和时频领域具有不可替代性。
五、射频器件稳定度评估的工程实践
5.1 测试系统架构
典型评估系统包含时间间隔计数器(采样率≥1 MSa/s)、相位噪声分析仪和恒温控制单元。以某型铷原子钟测试为例:
采集1小时频率数据,采样间隔τ₀=1 s;
计算τ=1 s、10 s、100 s下的阿伦方差;
绘制σ_y(τ)曲线,识别主导噪声类型。
5.2 实际案例分析
对某商用恒温晶振(OCXO)测试结果:
结果表明,短期稳定度受热噪声限制,中长期漂移由1/f噪声主导。
六、性能优化策略与前沿进展
6.1 硬件补偿技术
温度补偿:采用TCXO(温补晶振)将温漂系数从5e-7/℃降至5e-9/℃;
电源噪声抑制:低压差线性稳压器(LDO)将电源纹波影响降低40 dB。
6.2 算法优化方向
重叠阿伦方差:通过数据复用提升低频噪声分辨率;
小波去噪:在频域分离噪声与有用信号,提升短期稳定度评估精度。
6.3 新兴应用场景
在量子通信领域,阿伦方差用于评估光频梳的长期稳定度;在6G太赫兹通信中,该方法被用于优化本地振荡器的相位噪声特性。
结论
阿伦方差通过构建频率稳定度的时域量化框架,解决了传统方法在噪声收敛性方面的局限。其双维度评估能力为射频器件设计提供了从元件选型到系统集成的全链路优化路径。与标准方差相比,阿伦方差在噪声类型辨识、时间尺度敏感性和工程适用性方面具有显著优势。随着5G-Advanced和6G对频率稳定度提出更高要求,阿伦方差与机器学习结合的噪声预测技术将成为未来研究方向。
参考资料来源与地址
IEEE标准文献
IEEE Std 1139-2008, IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology—Random Instabilities
经典教材
W. J. Riley, Handbook of Frequency Stability Analysis (NIST Special Publication 1065, 2008)
地址:NIST官方下载页面
时频计量研究论文
D. W. Allan, "Statistics of Atomic Frequency Standards," Proceedings of the IEEE, vol. 54, no. 2, 1966.
射频器件测试应用案例
J. Levine, A Review of Time and Frequency Transfer Methods, Metrologia, 2008.
地址:IOPscience链接
噪声分离算法进展
E. Rubiola, Phase Noise and Frequency Stability in Oscillators, Cambridge University Press, 2008.
地址:出版社官网
量子通信领域应用
L. S. Ma et al., "Optical Frequency Standards and Their Applications in Quantum Communication," Journal of Lightwave Technology, 2020.
6G太赫兹通信技术
3GPP TR 38.803, Study on Hotspot and In-Building Solutions for 5G and Beyond (2023).
地址:3GPP官方页面
